4. Funkce a jejich grafy

SageMath podporuje mnoho způsobů jak vytvářet všemožné typy grafů. Tato funkcionalita nám umožňuje graficky experimentovat s funkcemi a vizualizovat různé situace (např. testování správnosti řešení nerovností).

V tomto notebooku si ukážeme nástroje, bez kterých se při této činnosti neobejdeme. Jde o velmi rozsáhlou oblast.

4.1 Funkce plot

Nejjednodušším způsobem, jak vizualizovat funkci, je vytvoření odpovídajícího symbolického výrazu s jednou symbolickou proměnnou a použití příkazu plot. Předveďme si tento postup na jednoduchém příkladě.

# Buď x symbolická proměnná.
var('x')
# Graf funkce 1/x * \sin(x^2) pro x z intervalu <1, 15>.
plot(1 / x * sin(x^2), (x, 1, 15))

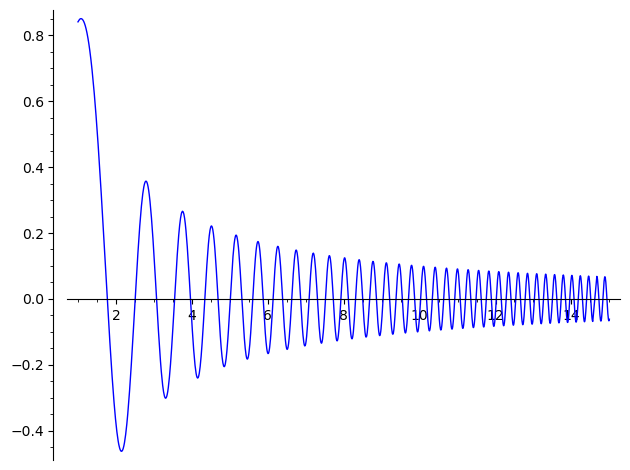
Funkce plot si, jak vidíme, poradí s výrazem a rozsahem pro symbolickou proměnnou (zde x). Můžeme jí ale předat přímo i funkci.

f(x) = sin(x) / x
show(f)           # všimněte si rozdílu mezi funkcí
show(f(x))        # a funkční hodnotou.

\(\displaystyle x \ {\mapsto}\ \frac{\sin\left(x\right)}{x}\)

\(\displaystyle \frac{\sin\left(x\right)}{x}\)

Nyní můžeme vynechat explicitní uvedení nezávisle proměnné.

plot(f, (0, 30))

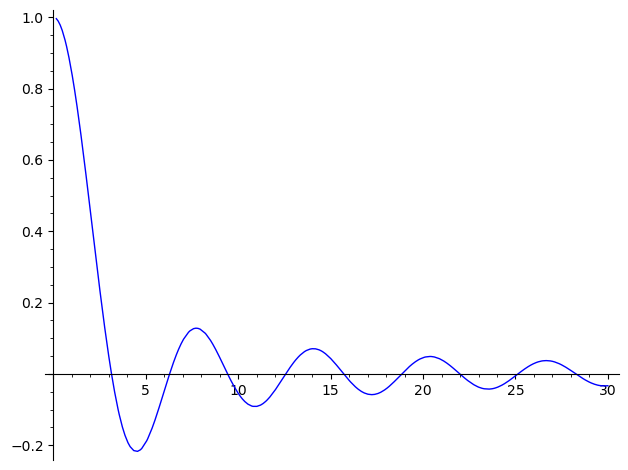
SageMath nám umožňuje vyladit i ostatní parametry grafu. V následující ukázce si ukážeme několik užitečných parametrů. Interně SageMath k tvorbě grafů využívá mocnou Pythonovskou knihovnu matplotlib. Doporučuji prozkoumat dokumentaci funkce plot.

plot(1 / x * sin(x^2), (x, 1, 15),
    ymin = -1, ymax = 1,                  # rozsah svislé osy
    thickness = 2,                        # tloušťka křivky
    rgbcolor = 'red',                     # barva
    axes_labels = ['$x$', '$y=f(x)$'],    # popisky os, lze využívat LaTeX
    tick_formatter = 'latex',             # cejchování os stejným fontem jako popisky os
    legend_label = '$y = \\sin(x^2)/x$',  # legenda (vhodné při kombinování více grafů)
    gridlines = True,                     # automatická mřížka
    figsize = 4)                          # velikost výsledného obrázku

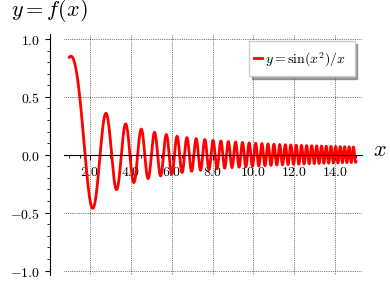
Občas je potřeba přesně specifikovat na kterých místech se mají osy cejchovat (typicky u trigonometrických funkcí). V následující ukázce grafu funkce arkus sinus si uážeme jak na to.

plot(arcsin(x), (x, -1, 1),
    ymin = -pi/2, ymax = pi/2,
    thickness = 2, rgbcolor = 'green',
    axes_labels = ['$x$', '$y$'], tick_formatter = 'latex',
    legend_label = '$y = \\arcsin(x)$',
    ticks = [[-1, -1/2, 1/2, 1],[-pi/2, -pi/4, pi/4, pi/2]], # cejchování os
    gridlines = True,
    figsize = 6)

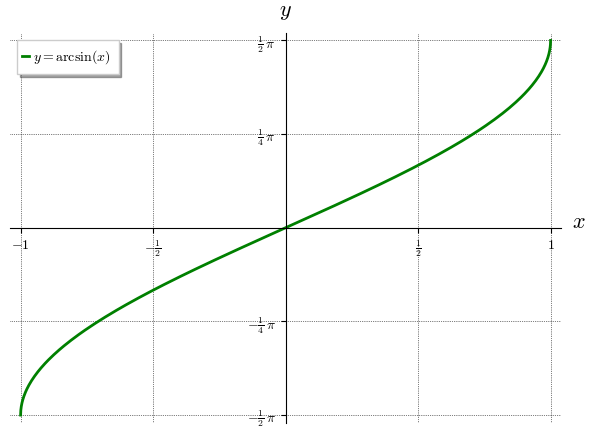
Funkce plot akceptuje i obyčejnou Pythonovskou funkci, která vrací číselné výsledky. Syntaxe je jen nepatrně odlišná (neuvádí se nezávisle proměnná). Následující funkce představuje numerickou aproximaci inverzní funkce k funkci \(g(x) = x e^x\), \(D_g = \langle -1, +\infty)\), tzv. Lambertovy funkce. Její implementace níže je reklamou na Newtonovu metodu, kterou budeme probírat později během semestru.

def lambert(z):
    """
        Naivní implementace Lambertovy funkce, tedy inverze
        k g(w) = w*exp(w), kde w > -1. Výpočet pomocí Newtonovy
        metody s očekávanou přesností na 5 cifer za desetinnou
        tečkou.
        
        PS: Na takovéto výpočty právě Python není nejlepší volba,
        toto je ale _demonstrační_ notebook, jehož pointa je jinde.
    """

    # Je argument "z" z definičního oboru?
    if z <= -1/e:
        raise ValueError('Argument není v definičním oboru Lambertovy funkce!')

    # Přesnost a iterátor rekurentní posloupnosti.
    eps = 1e-6
    newton = lambda w: w - (w*exp(w) - z) / (exp(w) + w*exp(w))

    # První nástřel.
    if z < 0:
        y1 = -0.5
    elif z > 0:
        y1 = z/2
    else:
        return 0

    # Iterativní výpočet.
    y2 = newton(z)
    while abs(y1 - y2) > eps:
        y1,y2 = y2,newton(y2)

    return y2

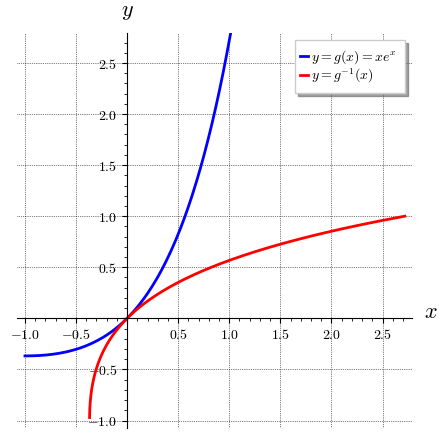
A nakonec graf s oběma funkcemi. Zde také ukazujeme, jak kombinovat více grafických objektů do jednoho. K tomu slouží operátor +. Různa nastavení grafiky (osy, velikost obrázku, atp.) stačí uvést jednou v prvním grafickém objektu.

fig1 = plot(x*exp(x), (x, -1, e),
    ymin = -1, ymax = e,
    thickness = 2, rgbcolor = 'blue',
    axes_labels = ['$x$', '$y$'], tick_formatter = 'latex',
    legend_label = '$y = g(x) = x e^x$', gridlines=True,
    figsize = 6, aspect_ratio = 1)

fig2 = plot(lambert, (-1/e, e),
    thickness = 2, rgbcolor = 'red',
    legend_label = '$y = g^{-1}(x)$')

fig1 + fig2

4.2 Funkce scatter_plot

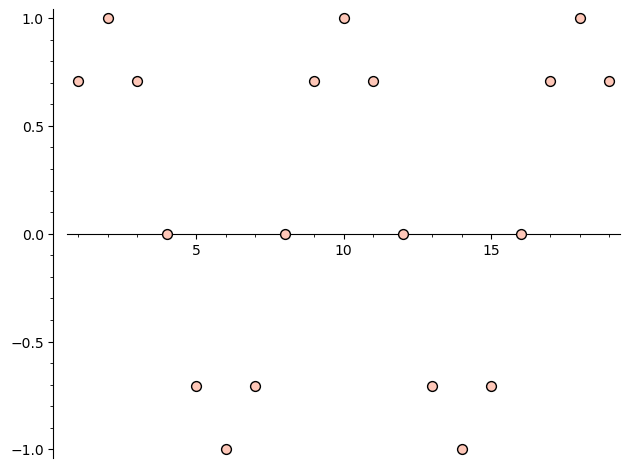
Nejen v BI-MA1 občas potřebujeme vizualizovat posloupnost \((a_n)_{n=1}^\infty\). K tomu se výše zmíněná funkce plot příliš nehodí. Diskrétní hodnoty lze snadno zobrazovat pomocí funkce scatter_plot. Vezměme například posloupnost s členy \(a_n = \sin\left(\frac{\pi n}{4}\right)\), \(n \in \mathbb{N}\).

a(n) = sin(pi * n / 4)

show(a)

\(\displaystyle n \ {\mapsto}\ \sin\left(\frac{1}{4} \, \pi n\right)\)

V tento moment SageMath o "diskrétnosti" proměnné n nic neví, my ovšem ano. Graf této posloupnosti, tedy množinu bodů tvaru \((n, a_n)\), \(n\in\mathbb{N}\), můžeme vizualizovat ve dvou krocích: napočteme odpovídající hodnoty posloupnosti a zobrazíme je pomocí funkce scatter_plot.

Nejprve vytvoříme list s požadovanými prvky (a zobrazíme si první čtyři):

points = [(n, a(n)) for n in range(1, 20)]

show(points[0:4])

\(\displaystyle \left[\left(1, \frac{1}{2} \, \sqrt{2}\right), \left(2, 1\right), \left(3, \frac{1}{2} \, \sqrt{2}\right), \left(4, 0\right)\right]\)

A poté body v tomto listu vizualizujeme pomocí scatter_plot.

scatter_plot(points)

Parametry grafu můžeme kontrolovat analogickým způsobem jako u plot.

4.3 Grafy funkcí dvou proměnných

V BI-MA2 budeme pracovat s funkcemi více proměnných. Pokud se budeme bavit o dvou proměnných, pak je poměrně snadné takové funkce vizualizovat, jejich graf je nyní plocha v trojrozměrném prostoru. V následujících buňkách nejprve definujeme druhou symbolickou proměnnou \(y\) a poté vykreslíme graf funkce \(f(x, y) = \sin(x)\sin(y) / \sqrt{x^2 + y^2}\).

var('y')

y

plot3d(sin(4*x) * sin(3*y) / sqrt(x^2 + y^2), (x, -5, 5), (y, -5, 5), plot_points=100)