5. Limity posloupností a funkcí#
V tomto notebooku se budeme věnovat jednomu z ústředních témat BI-MA1 - výpočtu limit funkcí a posloupností.
5.1 Výpočet pomocí limit#
Pokud chceme pomocí SageMath (ale i Mathematica) počítat limity posloupností je vhodné dát příslušnému počítačovému algebraickému systému na vědomí, že počítáme s diskrétní celočíselnou proměnnou. Obešli bychom se i bez toho, ale pak může dojít k překvapením.
var('n,x')
assume(n,'integer')
O proměnné \(x\) jsme žádný předpoklad neučinili. O \(n\) předpokládáme, že je celočíselná.
Potom SageMath korektně vyhodnotí následující příklad.
limit(sin(pi*n), n=+infinity)
0
Ve skutečnosti jde totiž o limitu konstantní posloupnosti \((0)_{n=1}^\infty\), pro každé celočíselné \(n\) totiž platí \(\sin(\pi n) = 0\). Naproti tomu se podívejme na následující výsledek.
limit(sin(pi*x), x=+infinity)
ind
Pokud o proměnné neučiníme žádný předpoklad, SageMath automaticky počítá s komplexní proměnnou, to pro nás většinou není problém, ale v některých situacích (viz dále) je to zásadní. Funkce \(x\mapsto\sin(\pi x)\) je periodická nekonstatní a nemá v nekonečnu limitu (o tom se nejlépe pčesvědčíme pomocí Heineho věty, viz níže).
Návratová hodnota ind je zkratkou slovíčka indeterminate, tedy neurčitý výraz.
V této situaci také musíme být opatrní.
Není jasné, jestli daná funkce/posloupnost skutečně limitu nemá, nebo jen algoritmus není schopen rozhodnout.
Všimněte si, že dvě předchozí buňky se vlastně neliší, až na označení proměnné.
Zásadní rozdíl je předpoklad zadaný pomocí assume v první buňce.
Seznam aktuálních předpokladů lze vypsat pomocí metody assumptions a smazat pomocí forget.
assumptions()
[n is integer]
5.2 Nekonečna a jednostranné limity#
Na chvíli se ještě zastavme u funkce limit.
K zápisu nekonečna lze vedle infinity použít i zkrácené oo (dvě malá "o" vedle sebe).
Pod infinity i oo SageMath "chápe" symbol \(+\infty\) z BI-MA1, který podrobně reprezentuje řetězcem +Infinity.
Záporné nekonečně pak znázorňuje pomocí -Infinity:
oo
+Infinity
infinity
+Infinity
-oo
-Infinity
Alternativně mám k dispozici i hezký výpis pomocí LaTeXu:
show(oo)
show(-oo)
Algebraické operace s těmito objekty ne/probíhají tak jak jsme zvyklí:
oo + 50
+Infinity
(-2) * oo
-Infinity
10^10 / oo
0
Ale!
oo + (-oo)
---------------------------------------------------------------------------
SignError Traceback (most recent call last)
Cell In [13], line 1
----> 1 oo + (-oo)
File ~/src/sage/src/sage/structure/element.pyx:1230, in sage.structure.element.Element.__add__()
1228 cdef int cl = classify_elements(left, right)
1229 if HAVE_SAME_PARENT(cl):
-> 1230 return (<Element>left)._add_(right)
1231 # Left and right are Sage elements => use coercion model
1232 if BOTH_ARE_ELEMENT(cl):
File ~/src/sage/src/sage/structure/element.pyx:2374, in sage.structure.element.ModuleElement._add_()
2372 Generic element of a module.
2373 """
-> 2374 cpdef _add_(self, other):
2375 """
2376 Abstract addition method
File ~/src/sage/src/sage/rings/infinity.py:393, in AnInfinity._add_(self, other)
391 raise SignError("cannot add unsigned infinities")
392 if self._sign != other._sign:
--> 393 raise SignError("cannot add infinity to minus infinity")
394 return self
SignError: cannot add infinity to minus infinity
oo * 0
---------------------------------------------------------------------------
SignError Traceback (most recent call last)
Cell In [14], line 1
----> 1 oo * Integer(0)
File ~/src/sage/src/sage/structure/element.pyx:1516, in sage.structure.element.Element.__mul__()
1514 return (<Element>left)._mul_(right)
1515 if BOTH_ARE_ELEMENT(cl):
-> 1516 return coercion_model.bin_op(left, right, mul)
1517
1518 cdef long value
File ~/src/sage/src/sage/structure/coerce.pyx:1204, in sage.structure.coerce.CoercionModel.bin_op()
1202 self._record_exception()
1203 else:
-> 1204 return PyObject_CallObject(op, xy)
1205
1206 if op is mul:
File ~/src/sage/src/sage/structure/element.pyx:1514, in sage.structure.element.Element.__mul__()
1512 cdef int cl = classify_elements(left, right)
1513 if HAVE_SAME_PARENT(cl):
-> 1514 return (<Element>left)._mul_(right)
1515 if BOTH_ARE_ELEMENT(cl):
1516 return coercion_model.bin_op(left, right, mul)
File ~/src/sage/src/sage/structure/element.pyx:2641, in sage.structure.element.RingElement._mul_()
2639
2640 cdef class RingElement(ModuleElement):
-> 2641 cpdef _mul_(self, other):
2642 """
2643 Abstract multiplication method
File ~/src/sage/src/sage/rings/infinity.py:453, in AnInfinity._mul_(self, other)
451 if other > 0:
452 return self
--> 453 raise SignError("cannot multiply infinity by zero")
SignError: cannot multiply infinity by zero
Pozor, v některých případech dostaneme jako výstup příkazu limit (ale potenciálně i jiných příkazů) pouze Infinity.
Pak jde o komplexní nekonečno, v ten moment SageMath předstírá výpočet limity funkce/posloupnosti s komplexními hodnotami. Například:
limit(1 / x, x=0)
Infinity
Tento výsledek není v rozporu s BI-MA1, protože funkci \(1/x\) chápe jako funkci s hodnotami v \(\mathbb{C}\), kde lze rozumně zavést pouze jeden symbol nekonečna. V BI-MA1 pro rozšíření reálné osy striktně používáme pouze symboly \(+\infty\) a \(-\infty\), pozorný student si toho jistě všiml.
Dobře, dokážeme ale ze SageMath v tomto případě dostat odpověď, který by více odpovídala tomu, co očekáváme? Přdpoklad o reálnosti \(x\), který jsme doposud neučinili, nám nepomůže. "Problém" pramení z oboru hodnot dané funkce.
assume(x, 'real')
limit(1 / x, x=0)
Infinity
Funkce limit přijímá několik nepovinných parametrů, v tento okamžik oceníme dir, pomocí kterého vynutíme výpočet limit zleva (- nebo left) nebo zprava (+ nebo right):
limit(1 / x, x=0, dir='+')
+Infinity
limit(1 / x, x=0, dir='-')
-Infinity
Tento výsledek se nám již líbí! Naše grafická intuitivní představa je totiž následující:
plot(1 / x, (x, -5, 5),
ymin = -10, ymax = 10,
detect_poles = True,
axes_labels = ["$x$", "$y$"],
legend_label = "$f(x) = 1/x$",
gridlines = True,
figsize = 5
)
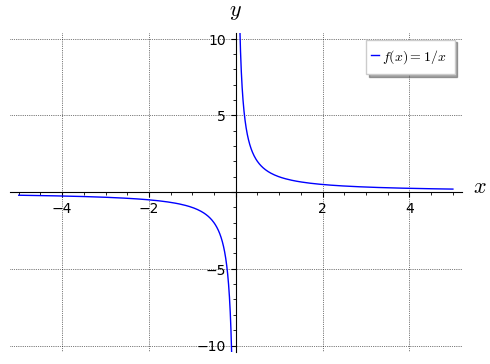
Limita
neexistuje (v BI-MA1 smyslu), protože jednostranné limity v nule jsou vzájemně různé.
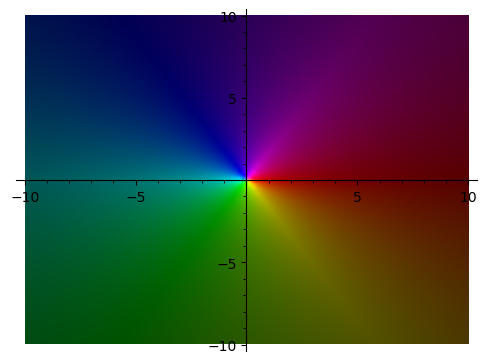
Čistě pro zajímavost, graf komplexní funkce komplexní proměnné \(f(z) = \frac{1}{z}\), \(D_f = \mathbb{C} \smallsetminus \{0\}\) vypadá následovně. Pokud se komplexní proměnná \(z\) blíží bodu \(0\), pak \(\frac{1}{|z|}\) roste nadevšechny meze (v grafu je toto vyjádřeno "světlostí"), což přesně odpovídá tvrzení, že v bodě \(0\) má limitu \(\infty\).
complex_plot(lambda z: 1 / z, (-10, 10), (-10, 10), figsize=5)
5.3 SageMath si poradí se známými limitami#
Následující limitu posloupnosti známe z přednášky,
SageMath nám dá očekávaný výsledek, Eulerovo číslo.
limit((1 + 1/n)^n, n=oo)
e
Častým omylem založeným na částečném limitění je tvrzení, že tato limita má hodnotu 1. Tato špatná intuice pramení v provedení několika nezávislých výpočtů limit (proto částečné), pro které nemáme žedné opodstatnění v teorii. Tento příklad je pěkný protipříklad k takovémuto postupu. Tj. \(1 + \frac{1}{n}\) má limitu \(1\), že? A \(1^n\) má limitu \(1\)? Ano, ale ne!
Eulerovo číslo je zde skutečně správným výsledkem. Podívejme se třeba i na hodnoty příslušné posloupnosti a její graf.
a = [ (1 + 1/n)^n for n in range(1, 50) ]
table(columns=[range(1, 10), a[1:10], map(N, a[1:10])], header_row=["n", "$a_n$", "přibližně"])
| n | \(a_n\) | přibližně |
|---|---|---|
| \(1\) | \(\frac{9}{4}\) | \(2.25000000000000\) |
| \(2\) | \(\frac{64}{27}\) | \(2.37037037037037\) |
| \(3\) | \(\frac{625}{256}\) | \(2.44140625000000\) |
| \(4\) | \(\frac{7776}{3125}\) | \(2.48832000000000\) |
| \(5\) | \(\frac{117649}{46656}\) | \(2.52162637174211\) |
| \(6\) | \(\frac{2097152}{823543}\) | \(2.54649969704071\) |
| \(7\) | \(\frac{43046721}{16777216}\) | \(2.56578451395035\) |
| \(8\) | \(\frac{1000000000}{387420489}\) | \(2.58117479171320\) |
| \(9\) | \(\frac{25937424601}{10000000000}\) | \(2.59374246010000\) |
list_plot(a,
ymin=1.8, ymax=2.9, gridlines=True, axes_labels=["$n$", "$a_n$"],
ticks=[srange(0,50,5), [2,2.4,2.6,e,2.8]],
figsize=4
)
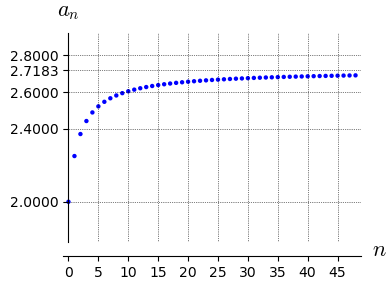
Vidíme, že jsme skutečně daleko od \(1\).
Pro úplnost připomeňme přibližnou hodnotu Eulerova čísla.
N(e, digits=100)
2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427
Další známé limity#
Zná SageMath hodnoty známých a důležitých funkcí (ve všech případech jde o neurčité výrazy \(0/0\))?
Příklad:
Výpočet v SageMath:
limit((e^x - 1) / x, x=0)
1
Grafická reprezentace, soustřeďte se na bod \(0\).
plot((exp(x) - 1) / x, (x, -2, 2),
ymin = -1, ymax = 5,
axes_labels = ["$x$", "$y$"],
legend_label = "$f(x) = (e^x - 1)/x$",
gridlines = True, figsize=5
)
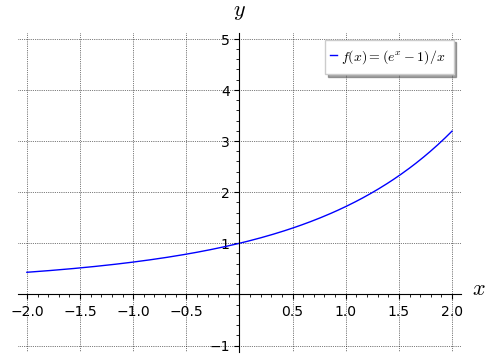
Příklad:
Výpočet v SageMath.
limit(ln(x + 1) / x, x=0)
1
Grafická ilustrace, soustřeďte se opět na bod \(0\).
plot(ln(x + 1) / x, (x, -1, 2),
ymin = -1, ymax = 5,
axes_labels = ["$x$", "$y$"],
legend_label = "$f(x) = \\ln(x+1)/x$",
gridlines = True, figsize=5
)
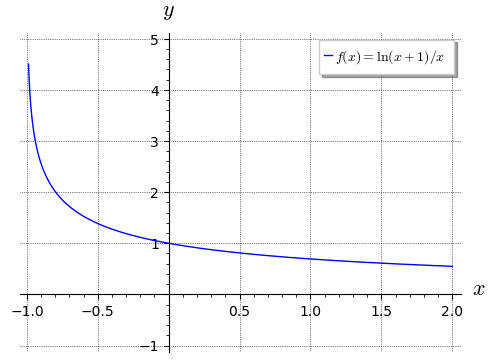
Příklad:
Spojité dodefinování funkce \(\frac{\sin(x)}{x}\) v bodě \(0\) je známé jako \(\mathrm{sinc}\).
limit(sin(x) / x, x=0)
1
plot(sin(x) / x, (x, -10, 10),
ymin = -1.5, ymax = 1.5,
axes_labels = ["$x$", "$y$"],
legend_label = "$f(x) = \\sin(x)/x$",
gridlines = True, figsize=5
)
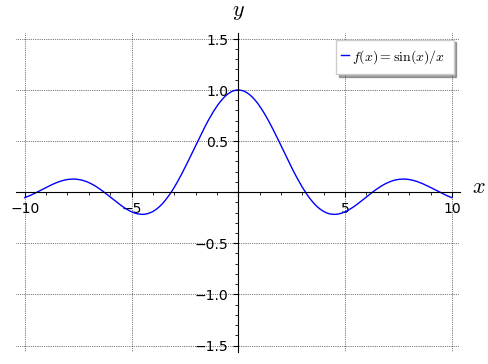
Příklad:
Podívejme se dále na funkci \(\mathrm{sgn}\), znaménko.
Její jednostranné limity v bodě \(0\) jsme prozkoumávali na přednášce.
V SageMath ji máme jako sign.
limit(sign(x), x=0, dir='+')
1
limit(sign(x), x=0, dir='-')
-1
limit(sign(x), x=0)
und
V tomto případě dostáváme und, tedy undefined. Většinou tato odpověď odpovídá situace, kdy limita neexistuje (což vidíme z hodnot jednostranných limit v \(0\)).
plot(sign(x), (x, -3, 3),
ymin = -1.5, ymax = 1.5,
axes_labels = ["$x$", "$y$"],
legend_label = "$f(x) = \\mathrm{sgn}(x)$",
gridlines = True, figsize=5
)
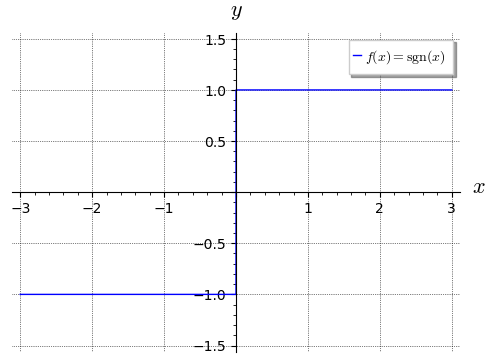
5.4 Problematický příklad#
Varování: nikdy bezmezně nevěřte počítačovým algebraickým systémů při výpočtu limit, existuje mnoho příkladů, na kterých selhávají. U SageMath (resp. Maxima na pozadí) například:
limit(x^(1/2 - sin(x)), x=oo)
+Infinity
Tato funkce ve skutečnosti ale limitu nemá! To můžeme snadno vidět vybráním dvou posloupností prvků z definičního oboru jdoucích do nekonečna, kterými budeme kontrolovat znaménko exponentu. Pro přehlednost si definujme naší funkci explicitně.
f(x) = x^(1/2 - sin(x))
A nyní se podívejme na její chování v bodech \(2\pi n\), \(n\in\mathbb{N}\):
limit(f(2*pi*n), n=oo)
+Infinity
list_plot([f(2*pi*n) for n in range(1,30)], axes_labels=["$n$", "$f(2\\pi n)$"], figsize=5)
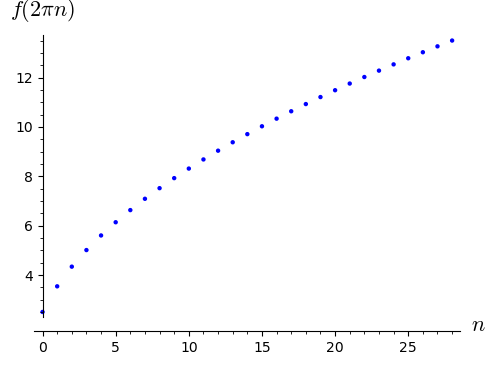
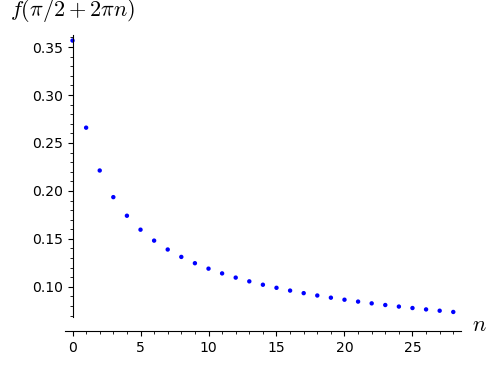
A poté v bodech \(\frac{\pi}{2} + 2\pi n\), \(n\in\mathbb{N}\).
limit(f(pi/2 + 2*pi*n), n=oo)
0
list_plot([f(pi/2 + 2*pi*n) for n in range(1,30)], axes_labels=["$n$", "$f(\\pi/2 + 2\\pi n)$"], figsize=5)
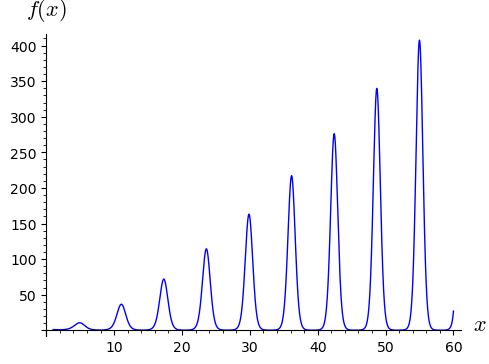
Celkový graf funkce.
plot(f(x), (x, 1, 60), axes_labels=["$x$", "$f(x)$"], figsize=5)
Vždy se při procvičování snažte prověřit (například graficky), jestli uvedený výsledek vypadá důvěryhodně. Pokud bychom chtěli argumentaci více vypilovat, museli bychom použít Heineho větu (zkuste!).
5.5 Heineho věta#
V neposlední řadě se nyní pokusíme využít SageMath ke grafickému znázornění Heineho věty, která studenty často trápí.
Stručně a lehce vágně řečeno, Heineho věta říká, že funkce \(f\) má v bodě \(a\) limitu \(b\), právě když pro každou posloupnost \((x_n)_{n=1}^\infty\) prvků z definičního oboru funkce \(f\) s limitou \(a\) a různých od \(a\) je limita posloupnosti \((f(x_n))_{n=a}^\infty\) rovna \(b\).
Tj. ještě více intuitivně: funkce \(f\) má v bodě \(a\) limitu \(b\), právě když funkční hodnoty \(f(x_n)\) jdou k \(b\) ať se k \(a\) hodnotami \(x_n\) blížíme jakýmkoliv způsobem.
Tuto větu nejčastěji používáme dvěma způsoby:
Víme, že \(\lim_{x \to a} f(x) = b\) (limita funkce), potom i \(\lim_{n\to\infty} f(x_n) = b\) (limita posloupnosti) pro nějakou konkrétní posloupnost \((x_n)_{n=1}^\infty\) s limitou \(a\) (s členy z \(D_f\) různými od \(a\)).
Pokud najdeme dvě posloupnosti \((x_n)_{n=1}^\infty\) a \((y_n)_{n=1}^\infty\) prvků z \(D_f\) různých od \(a\), ale majících limitu \(a\) (tj. dva způsoby, jak se blížit k \(a\)) a současně posloupnosti \((f(x_n))_{n=1}^\infty\) a \((f(y_n))_{n=1}^\infty\) mají různé limity, pak nutně limita funkce \(\lim_{x\to a} f(x)\) neexistuje.
Příklad: Na přednášce jsme odvodili limitu funkce
Pokud zvolíme napříkald posloupnost \(x_n = 2n\), pak díky Heineho větě takřka automaticky i víme, že
Označme si pro přehlednost konkrétní funkci:
f(x) = (1 + 1/x)^x
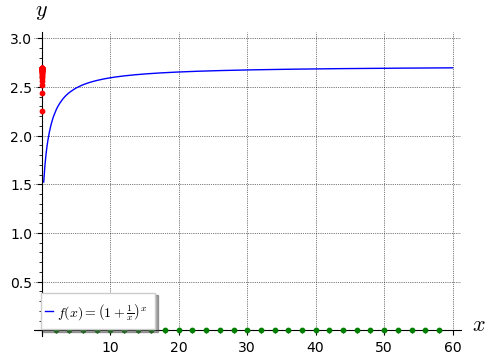
Následující obrázek obsahuje graf funkce \(f\) (modrá křivka) a dále i body posloupnosti \((2n)_{n=1}^\infty\) (zelené body) a body posloupnosti \((f(2n))_{n=1}^\infty\) (červené body). Bavíme se o limitě této funkce v nekončenu, jaké limity mají uvedené posloupnosti? Promyslete si tento obrázek v kontextu Heineho věty.
g1 = plot(f(x), (x, 0, 60), axes_labels = ["$x$", "$y$"],
figsize = 5, gridlines = True, ymin = 0, ymax = 3,
legend_label = "$f(x) = \\left( 1 + \\frac{1}{x} \\right)^x$",
)
g2 = scatter_plot([(2*n, 0) for n in range(1, 30)], markersize = 10,
facecolor = 'green', edgecolor = 'green'
)
g3 = scatter_plot([(0, f(2*n)) for n in range(1, 30)], markersize = 10,
facecolor = 'red', edgecolor = 'red'
)
g1 + g2 + g3
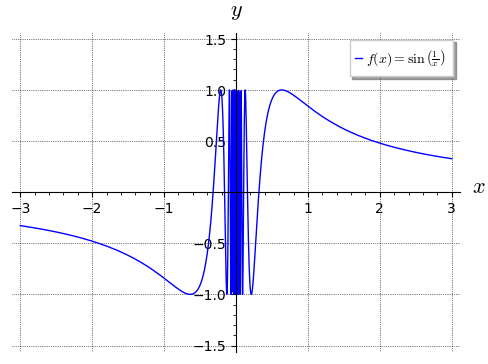
Příklad: Na přednášce jsme pomocí Heineho věty zkoumali chování funkce
pro \(x \to 0\). Dle SageMath jde o neurčitý výraz:
f(x) = sin(1 / x)
limit(f(x), x=0)
ind
Z grafu je zřejmé, že u nuly nastává problém:
plot(f(x), (x, -3, 3), axes_labels = ["$x$", "$y$"],
figsize = 5, gridlines = True, ymin = -1.5, ymax = 1.5,
legend_label = "$f(x) = \\sin\\left( \\frac{1}{x} \\right)$"
)
Zdá sem, že snadno vymyslíme dva způsoby, jak se s proměnnou \(x\) blížit k nule tak, aby funkční hodnoty šly k různým hodnotám:
\(x_n = \frac{1}{2\pi n} \to 0\),
\(y_n = \frac{1}{2\pi n + \frac{\pi}{2}}\).
V prvním případě jsou funkční hodnoty \(f(x_n)\) nulové, limita obrazů je rovna \(0\). Na následujícím obrázku pomocí puntíků znázorňujeme body \((x_n, f(x_n))\), jde tedy o lehce jiný pohled na věc než v předchozím příkladě.
g1 = plot(f(x), (x, 0, 0.5), axes_labels = ["$x$", "$y$"],
figsize = 5, gridlines = True, ymin = -1.5, ymax = 1.5,
legend_label = "$f(x) = \\sin\\left( \\frac{1}{x} \\right)$"
)
g2 = scatter_plot([(1/(2*pi*n), f(1/(2*pi*n))) for n in range(1, 30)], markersize = 5,
facecolor = 'red', edgecolor = 'red'
)
g1 + g2
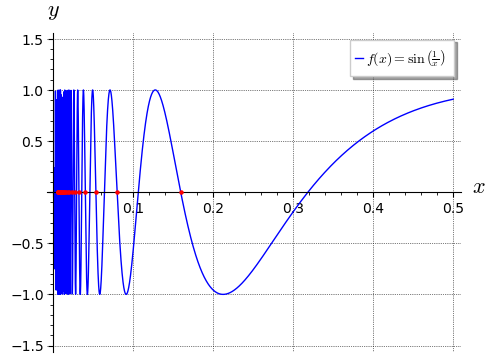
V druhém případě jsou funkční hodnoty ale všechny rovné \(1\):
g1 = plot(f(x), (x, 0, 0.5), axes_labels = ["$x$", "$y$"],
figsize = 5, gridlines = True, ymin = -1.5, ymax = 1.5,
legend_label = "$f(x) = \\sin\\left( \\frac{1}{x} \\right)$"
)
g2 = scatter_plot([(1/(2*pi*n + pi/2), f(1/(2*pi*n + pi/2))) for n in range(1, 30)], markersize = 5,
facecolor = 'red', edgecolor = 'red'
)
g1 + g2
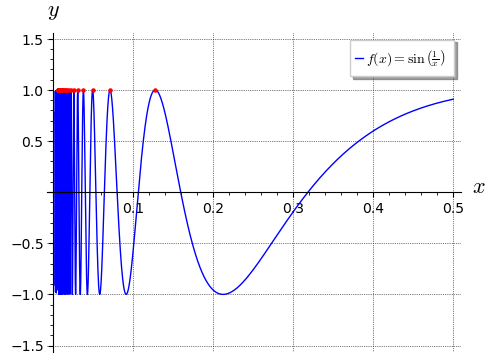
5.6 Kdo počítá??#
Doposud jsme v tomto notebooku výsledky připisovali programu SageMath. Ve skutečnosti ale výpočet limit v předchozích příkladech na pozadí prováděl počítačový algebraický systém Maxima.
Pomocí nepovinného argumentu algorithm (ne zcela výstižné pojmenování) lze vynutit výpočet i v jiném počítačovém algebraickém systému, např. Sympy.
limit(n^(1/n), n=oo, algorithm='sympy')
1
Nebo giac, který pod kapotou používá GeoGebra.
limit(x^2 + sin(x), x=oo, algorithm='giac')
+Infinity
Možnosti každého z těchto nástrojů jsou různé.
